1: Uma visão geral
A primeira etapa da aprendizagem e até mesmo de um projeto que venha a ser implementado de qualquer tipo de filtro, independentemente qual seja ele, passa, obrigatoriamente, pelos Filtros Passivos. Eles são a base construtiva e o modelo fundamental para análises preliminares.
Aperfeiçoamentos ou, tecnicamente, aproximações como Filtros Butterworth ou Filtros Bessel, entre outros, são modelos e projetos práticos, com implementação real, que têm, seus fundamentos em Filtros Passivos e Filtros Ativos. Esses últimos têm por fundamento os Filtros Passivos.
Assim, não importa o que se faça de mais sofisticado e o tipo de software que seja empregado, a questão é que tudo parte dos Filtros Passivos. Os Filtros Passivos assim são denominados porque utilizam elementos passivos que não alteram a resposta, ou, em outras palavras, a presença dos elementos constituintes não influencia a resposta final. São elementos passivos os resistores, os capacitores e os indutores, todos eles a base e fundamento da Engenharia Elétrica e Engenharia Eletrônica.
Por questões de um padrão do tipo “senso comum” o Filtro Passa Baixa do tipo RC é utilizado para compor os estudos preliminares para as diversas aproximações e/ou métodos para projetos. Assim é feito porque facilita comparações quanto às respostas para um mesmo modelo quando utilizadas metodologias diferentes. Mesmo que o padrão usado seja o Filtro Passa Baixa RC, outros modelos serão estudados nesse Artigo.
2: Parâmetros de Projeto
Para um Projeto de um Filtro Passivo é necessário definir dois parâmetros de Projeto que é a frequência de corte e a ordem do filtro. A partir desses parâmetros que nosso Filtro Passivo irá funcionar, conforme a topologia e as características pré-selecionadas pelo projetista. A marcha de Projeto para um Filtro Passivo é:
Parâmetro de Projeto:
1: Frequência ou frequências de corte, fc
2: Ordem do filtro, n.
De forma genérica um filtro de Ordem 2 é constituído de dois Filtros de Ordem 1 construídos de forma sequencial (em série). Assim, dois Filtros Passa Baixa RC em série de Ordem 1 conformam um Filtro Passa Baixa de Ordem 2. Isso serve para qualquer Ordem. Os Filtros Passivos têm ganho igual ou menor a 1. Quanto maior a Ordem, menor é o ganho.
Entenda-se que o Ganho (A) é a relação entre a tensão de saída e a tensão de entrada, e é medida na frequência de corte fc. Ou seja, para um Filtro, a ideia de que o sinal de saída seja menor que o sinal de entrada na frequência de corte fc é algo desejável para muitas aplicações. A equação abaixo apresenta a relação entre o Ganho (A) e a Ordem do Filtro (n). Essa equação é válida para filtros passivos.
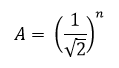
Tendo claro os parâmetros de projeto, a próxima etapa é projetar o Filtro. Antes, porém, é necessário compreender a teoria básica de Filtros para projetos. Alguns parâmetros ainda são necessários, entretanto, eles surgem em decorrência dos dois parâmetros apresentados.
Por fim, a Tabela 1 apresenta o Ganho de Filtros Passivos para Ordem de 1 até 10, na frequência de corte.
| Ordem – n | Ganho – A | Ordem – n | Ganho – A |
| 1 | 0,707 | 6 | 0,125 |
| 2 | 0,500 | 7 | 0,0883 |
| 3 | 0,353 | 8 | 0,0620 |
| 4 | 0,250 | 9 | 0,0440 |
| 5 | 0,176 | 10 | 0,0312 |
A maior desvantagem dos Filtros Passivos é que o volume físico do circuito aumenta na mesma proporção em que aumenta a Ordem do Filtro. Por vezes é necessário uma maior Ordem para poder obter o resultado desejado.
3: Fundamentação Teórica
Em um Filtro Passivo a frequência de corte e a ordem do filtro são os parâmetros de partida para um projeto. Do tipo de topologia utilizada é que parte toda a análise teórica, tendo em vista os parâmetros de projeto. A topologia utilizada permite extrair dois parâmetros circuitais, são eles:
- Função de Transferência
- Resposta da fase
A Função de Transferência (G) relaciona o sinal de saída com o sinal de entrada, conforme apresentado na equação 2. No caso o sinal em tela é a tensão elétrica.
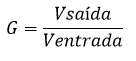
Como Filtros Passivos utilizam elementos passivos, ou seja, resistores, capacitores e indutores, é necessário conhecer a característica da tensão elétrica em cada um desses elementos. No caso do resistor a tensão está em fase com a corrente, logo, o ângulo de fase é 0º. No caso dos indutores a tensão elétrica está adiantada em 90º com relação à corrente elétrica, assim, o ângulo de fase é +90º. Por fim, no caso dos capacitores, a tensão elétrica está atrasada em 90º com relação à corrente elétrica, assim, o ângulo de fase é -90º. O ângulo de fase é, geralmente, indicado por α
- Capacitor – C: α = -90º
- Resistor – R: α = 0º
- Indutor – L: α = +90º
No caso do ângulo de fase α, ele é obtido a partir da relação entre o eixo imaginário com o eixo real. O eixo real acomoda os valores dos resistores e as impedâncias resistivas e o eixo imaginário acomoda os valores de impedância complexa, o que inclui capacitores e indutores. Na sequência algumas topologias.
Filtro Passivo Passa Baixa – Ordem 1

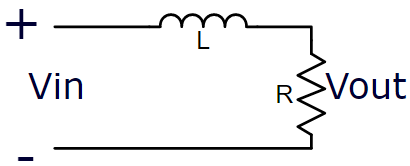
Filtro Passivo Passa Alta – Ordem 1
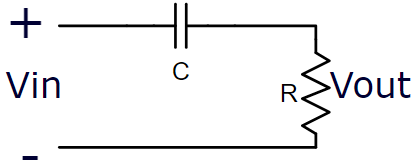
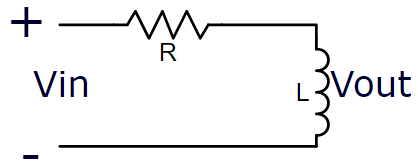
Filtro Passivo Passa Faixa – Ordem 1
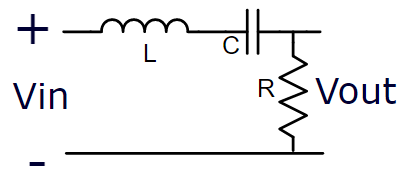
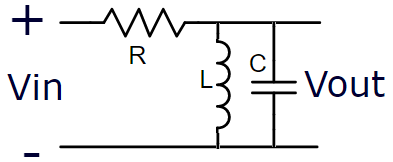
Filtro Passivo Rejeita Faixa – Ordem 1
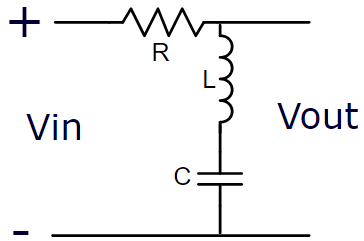
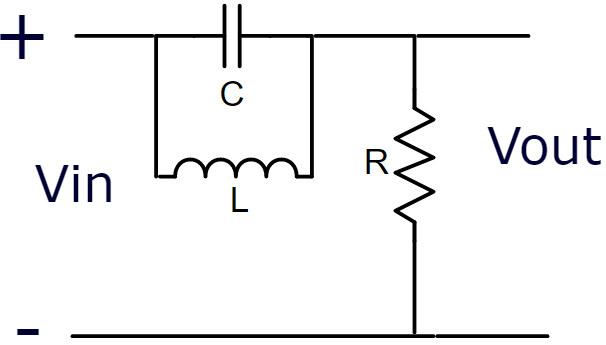
Filtro Passa Baixa – Ordem 2
4: Marcha de Projeto
Passo 1: Escolha do tipo de filtro (passa baixa; passa alta; passa faixa; rejeita faixa).
A escolha do tipo de filtro é feita através das necessidades circuitais apresentadas.
Passo 2: Escolha da topologia (RC, RL, RLC; série, paralelo).
A topologia permite ter uma gama de possibilidades. Permite, por exemplo, ter um filtro menor em tamanho físico (uso de capacitores) ou maior (uso de indutores). Também o uso de capacitores ou indutores é feito com base nos tipos de frequências que serão trabalhadas.
Passo 3: Escolha da Ordem do Filtro.
Quanto maior a Ordem do Filtro melhor o funcionamento do circuito. Entretanto, quanto maior a Ordem de um Filtro mais elementos estarão presentes no circuito. A Ordem de um Filtro é dada a partir da quantidade de elementos passivos presentes à exceção do resistor. Assim, um Filtro de Ordem 3 com topologia RC é um circuito que tem 3 capacitores (e 3 resistores). No caso de Filtros Ativos com uso de Amplificadores Operacionais, a quantidade de resistores difere da quantidade de capacitores (ou indutores). Somente no caso de Filtros Passivos a quantidade de resistores é a mesma da quantidade de capacitores (ou indutores).
Passo 4: Obter a Função de Transferência do circuito escolhido conforme passos 1, 2 e 3.
A Função de Transferência – G(ω) – é a relação entre o valor de saída e o valor de entrada, no caso esse valor faz referência à tensão elétrica.
Passo 5: Determinar o Ganho
O ganho – G – é dado a partir da Ordem do Filtro.
Passo 6: Determinar o ângulo de fase.
A partir dos valores do circuito é possível estimar o ângulo de fase – α.
Passo 7: Explicitar por gráficos a resposta do Filtro projetado.
5: Exemplo
Um eletroencefalograma para operar de forma mais adequada necessita isolar a frequência da rede de alimentação que vale, no local, 60 Hz. É sabido que as frequências aferidas estão abaixo dos 45 Hz. Projete um filtro que permita ler somente o intervalo de frequência necessária para o diagnóstico médico.
