1: Nossa motivação
Nas Escolas de Engenharia Eletricista, mais especificamente nas disciplinas dedicadas à Engenharia Elétrica, o estudo de Transformadores é disciplina clássica e certa. A disciplina é cursada e nela se é aprovado, entretanto, salvo algumas raras ocasiões, o conteúdo em si não é assimilado de forma mais profunda. Como reflexo disso é possível notar que em uma Pós Graduação poucos são os candidatos que se dedicam a essa área de estudo e; portanto, poucos são os profissionais que atuam como Projetistas de Transformadores Elétricos.
Ciente disso apresentamos um estudo partindo do elemento mais fundamental de qualquer projeto, a modelagem matemática e a abstração do modelo. Entretanto, não será somente apresentada uma abstração do modelo de um Transformador e sobre ela tecidos os comentários pertinentes. Não será feito dessa forma! Faremos diferente, vamos partir do nada, algo como “inventar a roda”. Tudo será construído para que o estudante e/ou profissional consiga entender, compreender e captar o significado de forma mais profunda de cada elemento que constitui a abstração e, por fim, a modelagem matemática. Assim, dessa forma, o entendimento sobre a modelagem matemática de um Transformador conseguirá transcorrer de forma mais fluida e garantir uma melhor experiência de aprendizagem.
Portanto; nossa motivação é ajudar que a modelagem matemática de um Transformador seja compreendido integralmente, partindo de uma abstração do modelo construído de forma sólida. E mais que isso, que seja possível motivar que profissionais se interessem por serem Projetistas de Transformadores, uma área, economicamente, muito atraente. Por fim, a Figura 1 mostra os elementos principais de um Transformador.

Para completar nossa análise inicial, algumas equações que norteiam as análises em um Transformador.
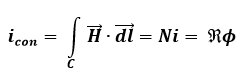
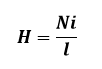
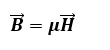
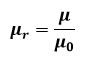
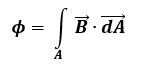
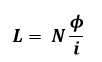
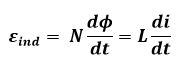
Onde:
icon: Corrente Concatenada [ A]
i: Corrente no Enrolamento [ A ]
H: Vetor Campo Magnético ou Intensidade Magnética [ A/m ]
l: Comprimento [ m ]
A: Área [ m2 ]
N: Número de espiras/voltas
ℜ: Relutância Magnética [ H-1 ]
μ0: Permeabilidade Magnética no Vácuo [ 4 10-7 H/m]
μ: Permeabilidade Magnética [ H/m ]
μr: Permeabilidade Relativa
Φ: Fluxo Magnético [ Wb = T/m2 ]
L: Indutância [ H ]
ε: Força Eletromotriz [ V ]
2: O ponto de partida
A primeira etapa é entender “o que entra e o que sai“. Isso serve para qualquer circuito na Engenharia. Seja um sistema hidráulico, seja um sistema térmico, seja um circuito elétrico, magnético ou eletrônico. Não importa, um engenheiro sempre precisa entender o que entra e o que sai do seu sistema ou circuito.
Portanto; nessa primeira etapa da construção de nosso raciocínio, apresentada na Figura 2, podemos afirmar que:
- O que entra: Tensão (Ein) e Corrente Elétrica (Iin)
- O que sai: Tensão (Eout) e Corrente Elétrica (Iout)
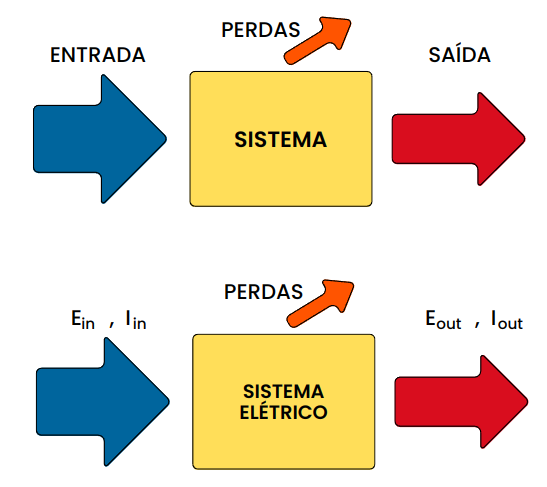
Logo, nossa primeira etapa de abstração, ainda que simplista, foi completada. Entretanto, como já é sabido na Engenharia, nem sempre o que entra também é o que sai. Há casos, porém, em que a entrada é igual à saída. Isso acontece, particularmente, em Sistemas Hidráulicos, onde a massa de fluido que entra é, no geral, a que sai, disso resulta que é possível definir a vazão volumétrica, já que o volume de entrada é o mesmo volume de saída, ainda que a velocidade do fluido e a área da seção não se mantenham. Entretanto, essa ideia não pode ser aplicada ao motor a combustão interna, por exemplo. Nesse caso, entra a energia química (combustível + ar) e juntamente com algumas condições específicas (pressão, relação estequiométrica e centelha – essa não existente para motores a diesel) permite a detonação e a transformação da energia química em energia motriz. Entretanto, não é toda energia química que se transforma em energia motriz, parte se transforma em energia térmica que no caso patente é considerada como perda de energia. Em um sistema realista, nós devemos considerar a entrada, a saída e as perdas, como demonstrado na Figura 3.
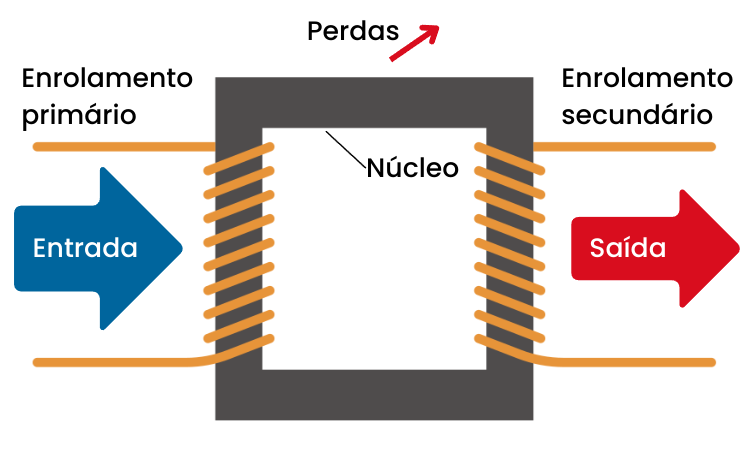
Figura 3: Esquema representativo em um transformador real
Assim também ocorre em uma máquina elétrica, em nosso caso, o Transformador Elétrico. As perdas também existem. Logo, a energia que entra não é a mesma que sai, de onde pode ser afirmado que:
Ein > Eout
Resta agora determinar as perdas. Para melhor compreensão das perdas o melhor é categorizá-las, ou seja, dividir conforme semelhanças, dentro de um grupo afim. Nessa toada as perdas elétricas em um Transformador podem ser categorizadas, em um primeiro momento, como:
- Perda nos enrolamentos
- Perdas no núcleo
Por enquanto, apenas a lógica foi aplicada e nada de novo foi apresentado. Portanto, o próximo passo é especificar cada uma das perdas em cada uma dessas categorias. Vamos começar nossa análise técnica.
3: Perda nos enrolamentos
Nossa primeira análise é feita nos enrolamentos do Transformador, sem considerar, por ora, o núcleo. No caso dos enrolamentos, estes são constituídos por fios de cobre. Nesse sentido os enrolamentos assumem um caráter resistivo quando da passagem da corrente elétrica. Assim, a primeira perda é do tipo resistiva nos enrolamentos e sua modelagem matemática e a abstração do modelo devem ser na forma de uma resistência elétrica. A Figura 4 apresenta a modelagem matemática de um Transformador Elétrico, até então. É nosso primeiro passo. Importante destacar que a passagem da corrente elétrica em um condutor produz o Efeito Joule que não é nada mais que a elevação da temperatura do mesmo.
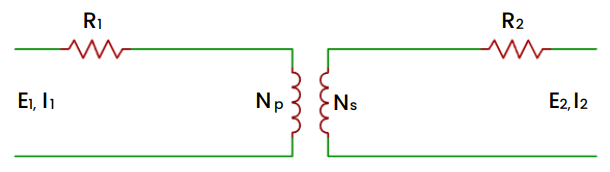
Essa foi a primeira etapa de nossa análise. Seguem as demais.
4: Perdas no núcleo
Nossa próxima etapa é avaliar as perdas no núcleo, sem mais se ater aos enrolamentos, análise que já fizemos. As perdas no núcleo têm relação, como o próprio nome sugere, ao núcleo e podemos apontar três tipos de perdas para esse caso, são elas:
- Perdas por histerese
- Perdas por correntes parasitas
- Perdas por dispersão
O próximo passo é estudar cada um desses subtipos.
4.1: Perdas por histerese
O primeiro que devemos entender é a respeito dos domínios magnéticos. Entenda-se por domínios magnéticos, ou somente domínios, as regiões onde há a presença de elétrons, e nessas regiões existe magnetismo inato. Portanto; cada elétron contribui com parte do campo magnético. Somados os campos magnéticos de cada região ou domínio magnético é possível obter o campo magnético total. A Figura 5 mostra a ideia dos domínios magnéticos conforme os tipos de materiais magnéticos, quando submetidos a um campo magnético.
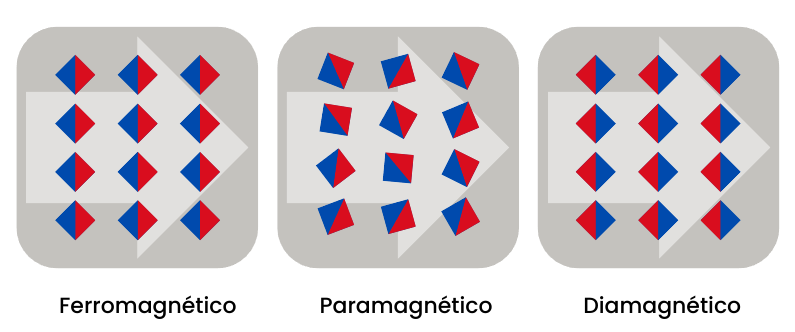
O núcleo dos transformadores são construídos por materiais ferromagnéticos. Esses materiais têm a característica de alinhar os domínios magnéticos quando da presença de corrente elétrica ou da presença de campo magnético externo. Os domínios magnéticos são vetores e a soma vetorial nessa região, a partir de cada domínio magnético individual, confere o valor final do campo magnético e do fluxo magnético nesta mesma região. Por serem vetores, além da intensidade importa a direção e o sentido. Como no caso dos materiais ferromagnéticos existe o alinhamento dos domínios magnéticos, o campo e fluxo magnéticos são bastante elevados porque a maioria dos domínios magnéticos estão alinhados na mesma direção e sentido.
Logo, o alinhamento dos domínios magnéticos, em materiais ferromagnéticos, permite aumentar o campo magnético e o fluxo magnético final. E isso é importante para um circuito magnético, caso de um Transformador Elétrico. Importante destacar que o fluxo magnético segue por dentro do núcleo.
Entretanto, a vantagem dos materiais ferromagnéticos não é absoluta. Acontece que um Transformador é submetido a tensões e correntes alternadas. Isso significa que o campo magnético e o fluxo magnético não se mantêm constantes ao longo do tempo. Logo, é natural concluir que os domínios magnéticos se alinhem a cada novo momento, conforme varia o sentido da tensão/corrente. Como o sentido da tensão e corrente alternadas varia no tempo, o mesmo ocorre com os domínios magnéticos que tendem a seguir esse movimento.
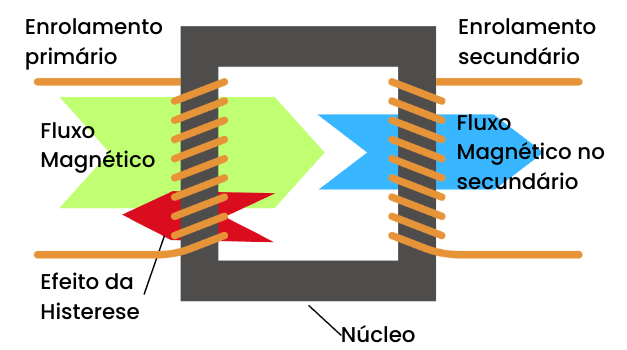
Ademais, esse processo de “ir e vir” fadiga, magneticamente, o material ferromagnético, fazendo com que o campo magnético e o fluxo magnético esperados teoricamente não sejam, de fato, o campo magnético e o fluxo magnético obtidos na realidade. Isso é o que se chama de histerese magnética. Assim, na histerese magnética há reorientação (de alguns) dos domínios magnéticos. Isso, além de reduzir o campo e fluxo magnéticos finais, ao haver oposição de alguns destes domínios, produz como resultado, calor. O calor gerado pela resistência nos enrolamentos também é gerado devido à histerese magnética no núcleo. São; portanto, duas formas de calor resultantes do próprio processo.
A Figura 6 mostra um gráfico típico de histerese magnética. A parte interna da curva representa a perda por histerese.
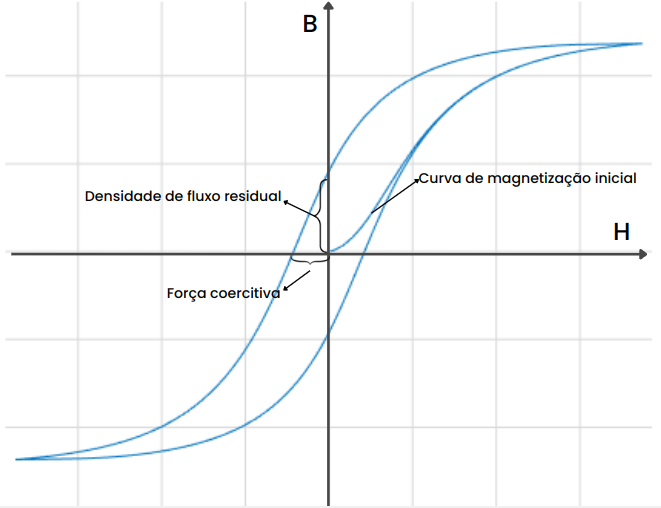
Assim, a Figura 7 apresenta a abstração de do modelo de um Transformador Elétrico que estudamos até então. Aqui já estão os dois elementos de perda analisados até o momento.
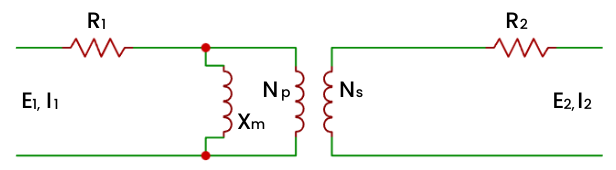
A análise por histerese magnética é uma perda que se refere à parte do fluxo magnético que não segue o caminho esperado, onde parte se desvia. Por estar relacionado com o fluxo magnético, está associado à ideia de reatância indutiva e a presença de um indutor como elemento de abstração, o que servirá para compor a modelagem matemática. A posição dessa reatância indutiva, indicada por XM, é devido à não passagem de parte do fluxo do lado 1 (entrada) para o lado 2 (saída). A Figura 8 mostra a ideia.
4.2: Perdas por correntes parasitas
A corrente elétrica que percorre os condutores gera um campo magnético B1 nos condutores. A corrente elétrica dos condutores é alternada. Isso faz com que o campo magnético B1 seja variável. Esse campo magnético B1 variável induz (Lei de Lenz) uma corrente elétrica no núcleo. Essa corrente elétrica induzida que circula no núcleo é também variável no tempo.
Essa corrente induzida é conhecida como Corrente Parasita; Corrente de Foucault ou ainda Corrente de Fuga. Como o material do núcleo é do tipo ferromagnético, ou seja, é um bom condutor elétrico, a circulação de corrente elétrica produz o Efeito Joule e causa, como consequência, calor. Tanto a corrente elétrica quanto o fluxo magnético fluem por dentro do núcleo. O fluxo magnético dentro do núcleo segue a Lei de Lenz, ou seja, é uma oposição ao sentido da corrente no enrolamento. A Figura 9 representa o que ocorre.
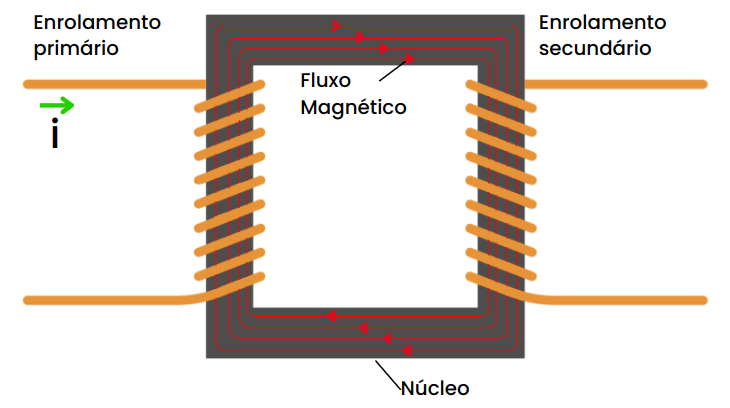
Para reduzir a intensidade da Corrente de Foucault há que aumentar a resistência ôhmica, reduzindo, assim, a corrente que circula no núcleo. Para isso é necessário avaliar a equação 8.
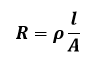
A partir da equação 8 é possível verificar que para aumentar a resistência ôhmica nós devemos aumentar o comprimento l ou reduzir a área transversal A. Na prática é a segunda opção que é aplicada com a adição de várias placas delgadas no lugar de um único bloco maciço espesso. Dessa forma é possível minimizar as Correntes de Foucault. A Figura 10 mostra a solução para o caso da Corrente de Foucault.
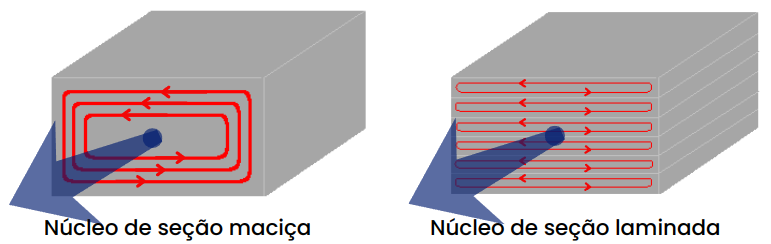
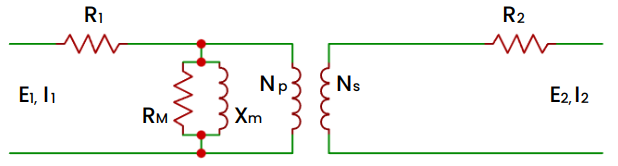
A Figura 11 mostra nossa abstração do modelo do Transformador Elétrico, até então. A posição da perda pelas Correntes de Foucault as quais produzem o Efeito Joule é no núcleo, já que é no núcleo que tudo acontece e é representado por RM. Há que destacar ainda que as Correntes de Foucault são, geometricamente, perpendiculares ao fluxo magnético que circula por dentro do núcleo, o qual é originado pela corrente que circula nos condutores.
A abstração para a modelagem matemática da perda por corrente parasita é na forma de uma resistência, uma vez que o elemento que o configura é a corrente elétrica. Ademais, o Efeito Joule causado é um efeito tipicamente de origem resistiva. É representado por RM. A posição RM é perpendicular à resistência R1. porque as Correntes de Foucault são perpendiculares ao fluxo magnético.
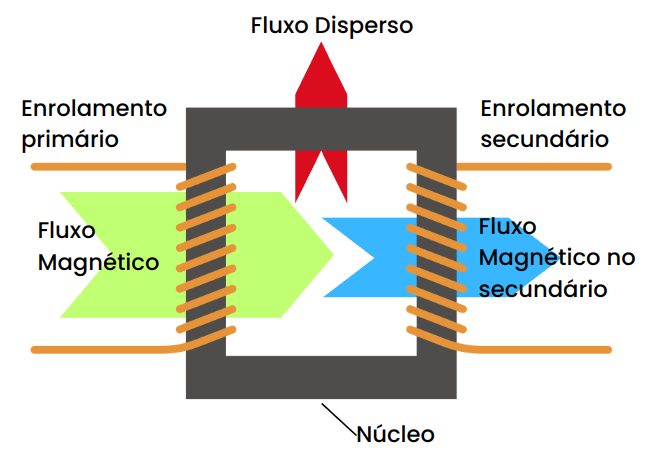
4.3: Perdas por dispersão
A partir da regra da mão direita, tendo claro o sentido da corrente elétrica é fácil perceber que o fluxo magnético tem direção perpendicular à seção transversal do núcleo e percorre o interior dele. Em um caso ideal todo o fluxo que circula no interior do núcleo chega ao seu destino. Entretanto, na prática não é o que ocorre. E essa diferença é chamada de Perda por dispersão e é modelada como uma perda de tipo indutiva pela própria natureza do fenômeno que ocorre. A dispersão ocorre entre o núcleo e o ar e é chamada de reatância de dispersão pelo ar. É representada por XL e está no mesmo sentido que o fluxo que percorre o interior do núcleo porque parte desse fluxo inicial é que se perde para o meio. A Figura 12 mostra a ideia dessa perda.
A Figura 13 mostra a modelagem matemática de um Transformador Elétrico, até então.
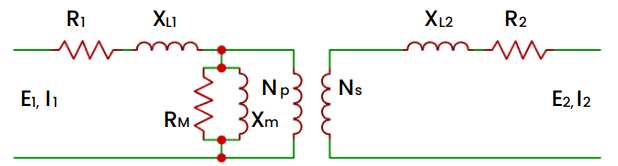
Essa modelagem é a mais usual, entretanto, não é a mais completa. Esse esquema serve para Transformadores Elétricos que trabalham até 1 KHz de frequência. Na prática, esse modelo serve para a maioria dos casos reais. Entretanto, nós avançaremos em direção a um modelo mais completo.
5: Uma modelagem mais completa
Até o momento todas as análises realizadas consideraram respostas de comportamento resistivo e indutivo. Há ainda respostas que comtemplam o comportamento capacitivo. Nessa seção é isso que vamos estudar.
A primeira etapa da análise foi feita utilizando a corrente elétrica como elemento principal de onde advém comportamentos resistivos e indutivos. Nessa seção vamos utilizar a tensão como elemento principal de onde advirá a capacitância. Conceitualmente a capacitância existe a partir da tensão elétrica e da presença de dois elementos próximos, geralmente, mas não sempre, placas planas e paralelas.
Nesta feita o primeiro elemento de capacitância ocorre entre os enrolamentos 1 (entrada) e 2 (saída). Como esses estão “frente a frente” e possuem uma tensão elétrica (diferente, uma vez que a tensão do primário é diferente da tensão do secundário), essa configuração produz uma capacitância entre enrolamentos e é representada por C12. É comum atribuir a capacitância C12 de forma a ter metade desta no início do enrolamento e outra metade ao fim. Adicionando esse efeito ao modelo anterior é possível construir a abstração do modelo do nosso Transformador até então estudado, o qual é apresentado na Figura 14.
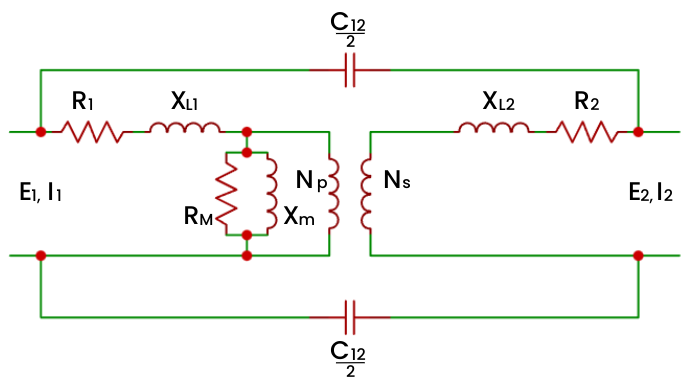
Nessa mesma lógica é possível antever que cada enrolamento, tanto o primário, como o secundário, é construído a partir de uma série de condutores de cobre enrolados e todos próximos entre si. Essa configuração produz “uma quantidade de capacitores” na mesma quantidade de pares que possam ser formados através de cada novo perímetro de enrolamento. Essa configuração como um todo produz a capacitância série no enrolamento, sendo representado como C1s para o caso do enrolamento primário, e C2s para o caso do enrolamento secundário. É capacitância em série porque envolve uma ação de duas partes do mesmo enrolamento. A Figura 15 mostra nossa nova configuração quanto à abstração.
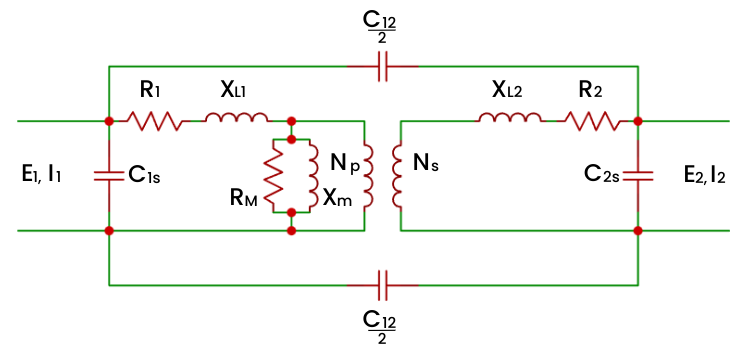
Uma outra capacitância que aparece é a capacitância do enrolamento com o terra. O terra é um elemento elétrico, ainda que seu potencial seja, idealmente, zero. Em Linhas de Transmissão a capacitância entre Linhas e a capacitância da Linha com o Neutro é algo considerado em projetos de Linhas de Transmissão. Assim, a capacitância do enrolamento com o terra também deve ser considerado em um Transformador.
Logo, a capacitância do enrolamento com o terra é representado como C1t e C2t para o primário e o secundário, respectivamente. É comum atribuir uma capacitância para a entrada e outra para a saída, o que resulta em metade para cada lado do mesmo enrolamento.
Para as análises de capacitância foram usados apenas os enrolamentos por serem considerados elementos distintos, tanto entre si como com relação ao outro enrolamento. Logo, não cabe análise de capacitância com relação ao núcleo. Ao fim, chega-se a um modelo mais completo, o qual apresentamos na Figura 16.
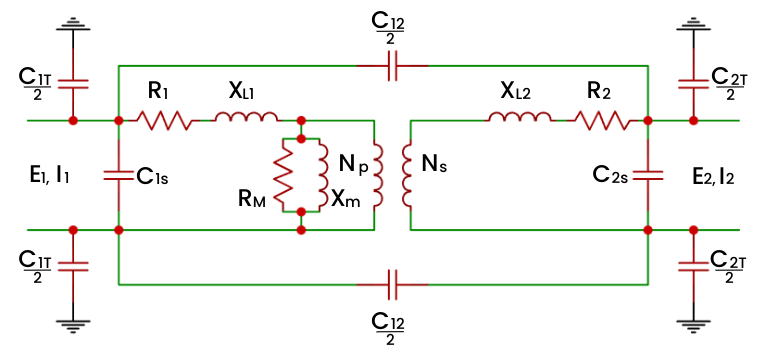
Essa é a modelagem matemática de um Transformador Elétrico mais realista. A aproximação da Figura 13 é útil para Transformadores que operem abaixo de 1 KHz. Para Transformadores que operem acima de 1 KHz é útil o modelo da Figura 16.
6: Resumo
Por fim, para completar o estudo apresentamos uma Tabela que resume as principais ideias da abstração que servirão para modelar matematicamente o Transformador.

A partir da abstração do modelo podemos desenvolver a modelagem matemática respectiva e, por ela, realizar análises de desempenho e desenvolvimento de projetos. Com um conhecimento apurado da abstração do modelo qualquer análise ou estudo se torna mais palpável.
